Establish the vector inequalities geometrically or otherwise : 

(b) |a+b| > ||a| −|b||

Let two vectors a and b be represented by the adjacent sides of a parallelogram OMNP, as shown in the given figure.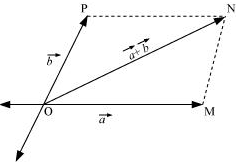 

 

Here, we have: 
| OM | = | a | 
| MN | = | OP | = | b | 
| ON | = | a + b | 
In a triangle, each side is smaller than the sum of the other two sides. 
Therefore, in ΔOMN, we have,
ON + MN > OM 
ON + OM > MN 
| ON | > | OM - OP |   (∵ OP = MN) 
| a + b | > | | a | - | b | |                 ...(iv) 
If the two vectors a and b act along a straight line in the same direction, then we can write: 
| a + b | = | | a | - | b | |                 ...(v) 
Combining equations (iv) and (v), we get: 
| a + b | ≥ | | a | - | b | |