Figure 3.25 gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude ? In which interval is the average speed greatest ? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

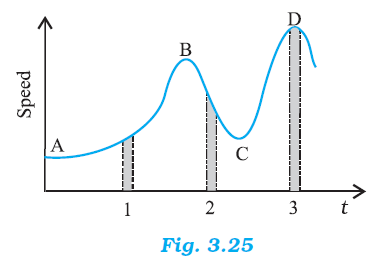
Acceleration is given by the slope of the speed-time graph.
Since the slope of the given speed-time graph is maximum in interval 2, the average acceleration will be the greatest in this interval.
The height of the curve from the time-axis gives the average speed of the particle.
In the given graph, it is clear that the height is the greatest in interval 3.
Hence, the average speed of the particle is the greatest in interval 3.
In interval 1:

The slope of the speed-time graph is positive. Hence, acceleration is positive. Similarly, the speed of the particle is positive in this interval.
In interval 2:
The slope of the speed-time graph is negative. Hence, acceleration is negative in this interval. However, speed is positive because it is a scalar quantity.
In interval 3:
The slope of the speed-time graph is zero. Hence, acceleration is zero in this interval. However, here the particle acquires some uniform speed. It is positive in this interval.
Points A, B, C, and D are all parallel to the time-axis. Hence, the slope is zero at these points. Therefore, at points A, B, C, and D, acceleration of the particle is zero.