☰
Correlation
Calculate height and weight of the students of a class.
|
Height (in inches) |
57 |
59 |
62 |
63 |
64 |
65 |
55 |
58 |
57 |
|
Weight in (Pounds) |
113 |
117 |
126 |
126 |
130 |
129 |
111 |
116 |
112 |
|
X |
dx (x-60) |
d2x |
y |
dy(y–120) |
d2y |
dxdy |
|
37 |
–3 |
9 |
113 |
–7 |
49 |
21 |
|
59 |
–1 |
1 |
117 |
–3 |
9 |
3 |
|
62 |
+ 2 |
4 |
126 |
+ 6 |
36 |
12 |
|
63 |
+ 3 |
9 |
126 |
+ 6 |
36 |
18 |
|
64 |
+ 4 |
16 |
130 |
+ 10 |
100 |
40 |
|
65 |
+ 5 |
25 |
129 |
+ 9 |
81 |
45 |
|
55 |
–5 |
25 |
111 |
–9 |
16 |
6 |
|
58 |
–2 |
4 |
116 |
–4 |
16 |
8 |
|
57 |
–3 |
9 |
112 |
–8 |
64 |
24 |
|
ΣdX = 0 |
Σd2X = 100 |
dy = 0 | d2y = 472 |
ΣdXd = 216 |
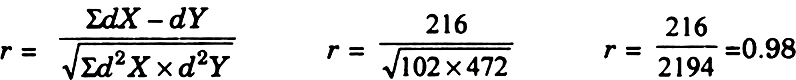
Sponsor Area
The unit of correlation coefficient between height in feet and weight in kgs is:
The range of simple correlation coefficient is:
If rxy is positive the relation between X an Y is of the type:
If rxy = 0 the variable X and Y are:
Of the following three measures which can measure any type of relationship:
If precisely measured data are available the simple correlation coefficient is:
Why is r preferrred to co-variance as a measure of association?
Can r lie outside -1 and 1 range depending on the type of data?
Does correlation imply causation?
When is rank correlation more precise than simple correlation coefficient?
Sponsor Area
Sponsor Area