☰
Correlation
We are given the percentage of marks secured by 5 students in Economics and Statistics calculate rank correlation.
|
Student |
Marks in Statistics (X) |
Marks in Economics (Y) |
Ranking in Statistics (Rx) |
Ranking in Economics (R)y |
(RD–R1) |
D2 |
|
A |
85 |
60 |
1 |
I |
0 |
0 |
|
B |
60 |
48 |
4 |
5 |
– 1 |
1 |
|
C |
55 |
49 |
5 |
4 |
1 |
1 |
|
D |
65 |
50 |
3 |
3 |
0 |
0 |
|
E |
75 |
55 |
2 |
2 |
0 |
0 |
|
Σ D2 = 2 |
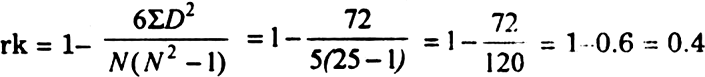
Sponsor Area
Can r lie outside -1 and 1 range depending on the type of data?
Does correlation imply causation?
When is rank correlation more precise than simple correlation coefficient?
Does zero correlation mean independenc?
Can simple correlation coefficient measure any type of relationship?
Collect the price of five vegetables from your local market everyday for a week. Calculate their correlation coefficient. Interpret the result.
List some variables where accurate measurement is difficult.
Interpret the values of r as 1, –1 and 0.
Why does rank correlation coefficient differ from Personian correlation co-efficient?
Measure the height of your classmates. Ask them the height of their benchmate:Calculate the correlation coefficient of these two variables. Interpret the result
Sponsor Area
Sponsor Area