Prove that the length of tangents drawn from an external point to a circle is equal.

Given: TP and TQ are two tangent drawn from an external point T to the circle C (O, r).


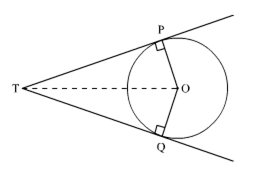
To prove: TP = TQ
Construction: Join OT
Proof: we know that a tangent to the circle is perpendicular to the radius through the point of contanct.
∴ ∠OPT = ∠OQT = 90^o
In Δ OPT  and ΔOQT
OT = OT  (common)
OP = OQ (radius of the circle)
∠OPT = ∠OQT (90^o)
∴ ∠OPT = ∠OQT (RHS congruence criterion)
⇒ TP = TQ (CPCT)
Hence, the length of the tangents drawn from an external point to a circle is equal.