☰
Symmetry
Sponsor Area
Give three examples of shapes with no line of symmetry.
What other name can you give to the line of symmetry of
(a) an isosceles triangle?
(b)a circle?
Give the order of rotational symmetry for each figure:
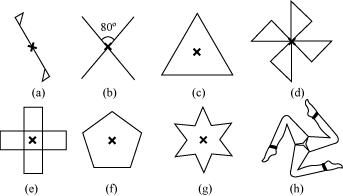
Name any two figures that have both line symmetry and rotational symmetry.
Draw, wherever possible, a rough sketch of
(i) a triangle with both line and rotational symmetries of order more than 1.
(ii) a triangle with only line symmetry and no rotational symmetry of order more than 1.
(iii) a quadrilateral with a rotational symmetry of order more than 1 but not a line symmetry.
(iv) a quadrilateral with line symmetry but not a rotational symmetry of order more than 1.
If a figure has two or more lines of symmetry, should it have rotational symmetry of order more than 1?
Fill in the blanks:
| Shape | Centre of Rotation | Order of Rotation | Angle of Rotation |
| Square |
– |
– |
– |
| Rectangle |
– |
– |
– |
| Rhombus |
– |
– |
– |
| Equilateral Triangle |
– |
– |
– |
| Regular Hexagon |
– |
– |
– |
| Circle |
– |
– |
– |
| Semi-circle |
– |
– |
– |
Name the quadrilaterals which have both line and rotational symmetry of order more than 1.
After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
Can we have a rotational symmetry of order more than 1 whose angle of rotation is
(i) 45°?
(ii) 17°?
Sponsor Area
Sponsor Area
