The Triangle and its Properties
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
Considering ΔOAB,
OA + OB > AB (i)
In ΔOBC,
OB + OC > BC (ii)
In ΔOCD,
OC + OD > CD (iii)
In ΔODA,
OD + OA > DA (iv)
Adding equations (i), (ii), (iii), and (iv), we obtain
OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA
2OA + 2OB + 2OC + 2OD > AB + BC + CD + DA
2OA + 2OC + 2OB + 2OD > AB + BC + CD + DA
2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
2(AC) + 2(BD) > AB + BC + CD + DA
2(AC + BD) > AB + BC + CD + DA
Yes, the given expression is true.
Sponsor Area
Some More Questions From The Triangle and its Properties Chapter
Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm (ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Take any point O in the interior of a triangle PQR. Is
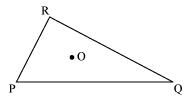
(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
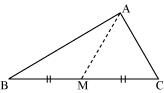
AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
ABCD is quadrilateral.
Is AB + BC + CD + DA >AC + BD?
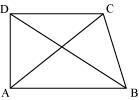
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC
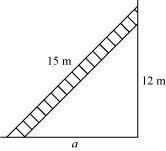
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area