☰
The Triangle and its Properties
Find the value of the unknown interior angle x in the following figures:
(i) x + 50° = 115° (Exterior angle theorem)
x = 115° − 50° = 65°
(ii) 70° + x = 100° (Exterior angle theorem)
x = 100° − 70° = 30°
(iii) x + 90° = 125° (Exterior angle theorem)
x = 125° − 90° = 35°
(iv) x + 60° = 120° (Exterior angle theorem)
x = 120° − 60° = 60°
(v) x + 30° = 80° (Exterior angle theorem)
x = 80° − 30° = 50°
(vi) x + 35° = 75° (Exterior angle theorem)
x = 75º − 35º = 40°
Sponsor Area
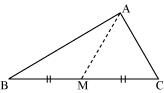
AM is a median of a triangle ABC.
Is AB + BC + CA > 2 AM?
(Consider the sides of triangles ΔABM and ΔAMC.)
ABCD is quadrilateral.
Is AB + BC + CD + DA >AC + BD?
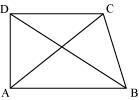
ABCD is quadrilateral.
Is AB + BC + CD + DA < 2 (AC + BD)?
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC
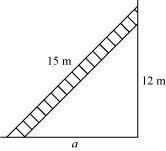
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm
(ii) 2 cm, 2 cm, 5 cm
(iii) 1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
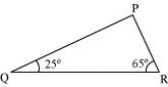
Angles Q and R of a ΔPQR are 25° and 65°.
Write which of the following is true:
(i) PQ2 + QR2= RP2
(ii) PQ2 + RP2= QR2
(iii) RP2 + QR2= PQ2
Sponsor Area
Sponsor Area