☰
✕

Constructions
Question
Wired Faculty App

In figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).



[Hint. Join AC.]

Answer

Given: ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. AQ intersects DC at P.
To Prove: ar(ΔBPC) = ar(ΔDPQ).
Construction: Join AC.
Proof: ∵ ΔQAC and ΔQDC are on the same base QC and between the same parallels AD and QC.

∴ ar(ΔQAC) = ar(ΔQDC)    ...(1)
Two triangles on the same base (or equal bases) and between the same parallels are equal in areas
⇒ ar(ΔQAC) – ar(ΔQPC)
= ar(ΔQDC) – ar(ΔQPC)
| Subtracting the same areas from both sides
⇒ ar(ΔPAC) = ar(ΔQDP)    ...(2)
∵ ΔPAC and ∵PBC are on the same base PC and between the same parallels AB and DC.
∵ ar(∵PAC) = ar(∵PBC)    ...(3)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
From (2) and (3),
ar(ΔPBC) = ar(ΔQDP)
⇒    ar(ΔBPC) = ar(ΔDPQ).

Sponsor Area

Some More Questions From Constructions Chapter

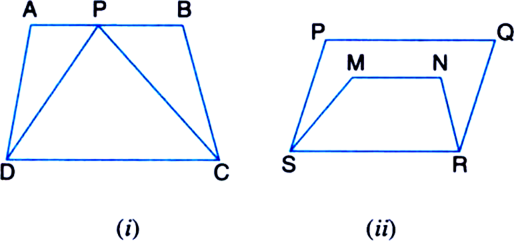
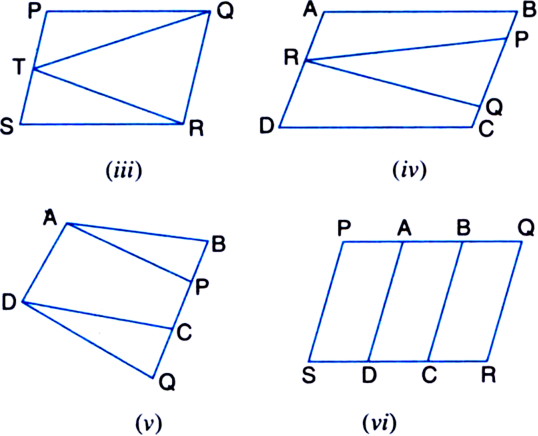
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.

Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.

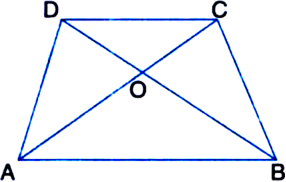
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).