☰
✕

Constructions
Question
Wired Faculty App

In figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).

Answer

Given: ABCD, DCFE and ABFE are parallelograms.
To Prove: ar(ΔADE) = ar(ΔBCF).
Proof: ∵ ABCD is a || gm
∴ AB || DC    ...(1)
| Opposite sides of a || gm are ||
∵    DCFE is a || gm
∴ DC || EF    ...(2)
| Opposite sides of a || gm are ||
From (1) and (2),
AB || EF    ...(3)
∵    ABCD is a || gm
∴ AD = BC    ...(4)
| Opposite sides of a || gm are equal
∵    ΔADE and ΔBCF are on equal bases (∵ AD = BC) and between the same parallels AB and EF.
□∴ ar(ΔADE) = ar(ΔBCF).
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in areas

Sponsor Area

Some More Questions From Constructions Chapter

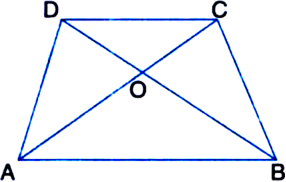
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).

Parallelograms on the same base and between same parallels are equal in area. Prove this.

ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

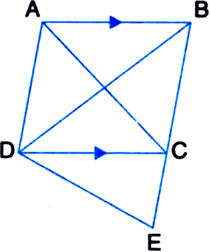
In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).

 In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)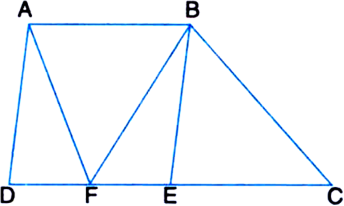

In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.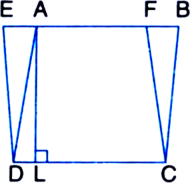

If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.