Constructions
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the comers to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
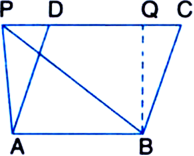
Let ABCD be the plot of land of the shape of a quadrilateral. Let the portion ADE be taken over by the Gram Panchayat of the village from one comer D to construct a Health Centre.
Join AC. Draw a line through D parallel to AC to meet BC produced in P. Then Itwaari must be given the land ECP adjoining his plot so as to form a triangular plot ABP as then
ar(ΔADE) = ar(ΔPEC).
Proof: ∵ ΔDAP and ΔDCP are on the same base DP and between the same parallels DP and AC.
∴ ar(ΔDAP) = ar(ΔDCP)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
⇒ ar(ΔDAP) – ar(ΔDEP)
= ar(ΔDCP) – ar(ΔDEP)
| Subtracting the same areas from both sides
⇒ ar(ΔADE) = ar(ΔPCE)
⇒ ar(ΔDAE) + ar(□ABCE)
= ar(ΔPCE) + ar(□ABCE)
| Adding the same areas to both sides
⇒ ar(□ABCD) = ar(ΔABP).
Sponsor Area
Some More Questions From Constructions Chapter
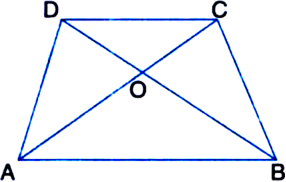
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).
Parallelograms on the same base and between same parallels are equal in area. Prove this.
ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).
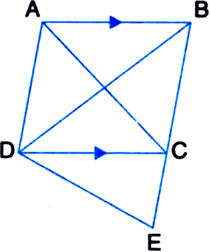
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)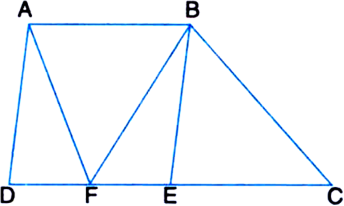
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.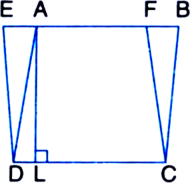
If a triangle and a parallelogram are on the same base and between the same parallels, then prove that the area of the triangle is equal to half the area of the parallelogram.
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area