Constructions
In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE).
Given: ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
To Prove: (i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE).
Proof: (i) ∵ ΔACB and ΔACF are on the same base AC and between the same parallels AC and
BF. [∵ AC || BF (given)]
∴ ar(ΔACB) = ar(ΔACF)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
(ii) From (i),
ar(ΔACB) = ar(ΔACF)
⇒ ar(ΔACB) + ar(□AEDC)
= ar(ΔACF) + ar(□AEDC)
| Adding the same areas on both sides ⇒ ar(ABCDE) = ar(□AEDF)
⇒ ar(□AEDF) = ar(ABCDE).
Sponsor Area
Some More Questions From Constructions Chapter
Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.
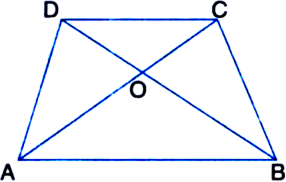
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).
Parallelograms on the same base and between same parallels are equal in area. Prove this.
ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).
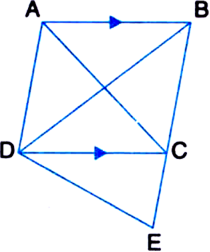
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)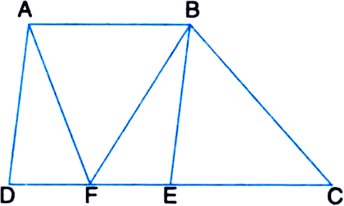
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.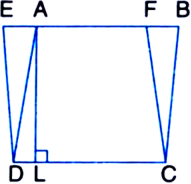
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area