Constructions
Question
In figure, E is any point on median AD of a ΔABC. Show that ar(ΔABE) = ar(ΔACE).
Answer
Given: E is any point on median AD of a ΔABC.
To Prove: ar(ΔABE) = ar(ΔACE).
Proof: In ΔABC,
∵ AD is a median. ∴ ar(ΔABD) = ar(ΔACD) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas
In ΔEBC,
∵ ED is a median.
∴ ar(ΔEBD) = ar(ΔECD) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get ar(ΔABD) – ar(ΔEBD)
= ar(ΔACD) – ar(ΔECD)
⇒ ar(ΔABE) = ar(ΔACE).
Sponsor Area
Some More Questions From Constructions Chapter
Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.
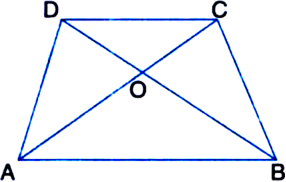
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).
Parallelograms on the same base and between same parallels are equal in area. Prove this.
ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).
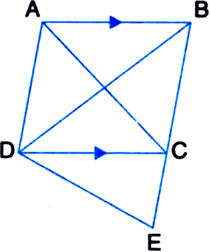
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)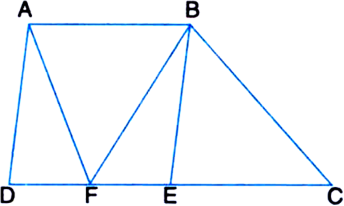
In the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL ⊥ DC. Prove that
(i) ar(ABCD) = ar(EFCD)
(ii) ar(ABCD) = DC x AL.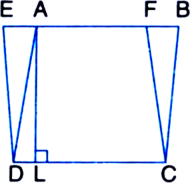
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area