☰
✕

Areas of Parallelograms and Triangles
Question
Wired Faculty App

BD and CE are the bisectors of ∠B and ∠C of an isosceles triangle ABC with AB = AC. Prove that BD = CE.

Answer

∵ AB = AC
∴ ∠ACB = ∠ABC
| Angles opposite to equal sides of ∆ABC
⇒    2∠2 = 2∠1
| ∵ CE and BD are the bisectors of ∠C and ∠B respectively
⇒    ∠2 = ∠1
⇒    BP = PC    ...(1)
| Sides opposite to equal angles of ∆PBC

In ∆BPE and ∆CPD,
BP = CP    | Proved above
∠EBP = ∠DCP    | Proved above
∠BPE = ∠CPD
| Vertically Opposite Angles
∴ ∆BPE ≅ ∆CPD    | ASA Axiom
PE = PD    | C.P.C.T.
⇒    PD = PE    ...(2)
Adding (1) and (2), we get
BP + PD = PC + PE
⇒    BD = CE.

Sponsor Area

Some More Questions From Areas of Parallelograms and Triangles Chapter

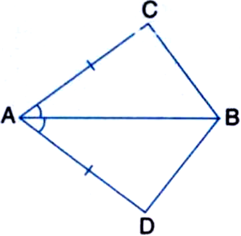
In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?

ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:

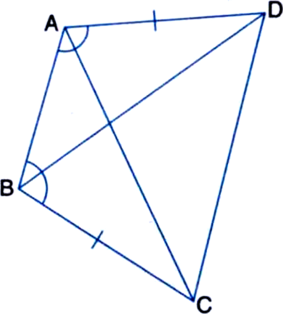
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

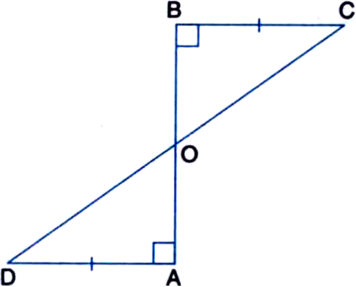
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

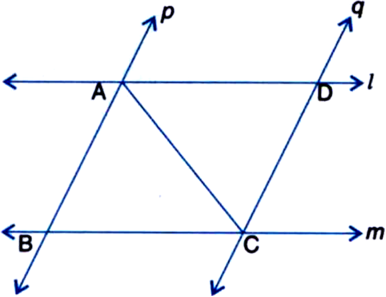
I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.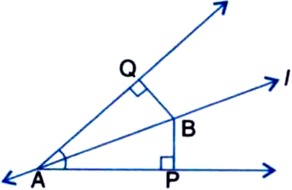

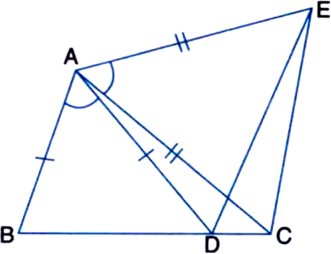
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

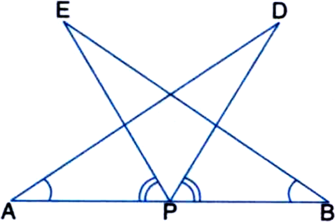
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

 

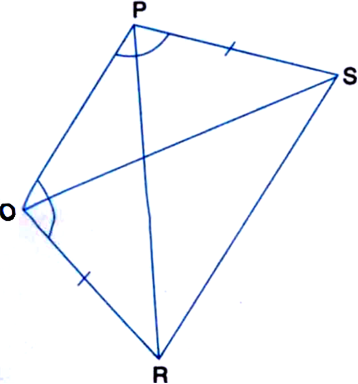
In figure, PS = QR and ∠SPQ = ∠RQP. Prove that PR = QS and ∠QPR = ∠PQS.

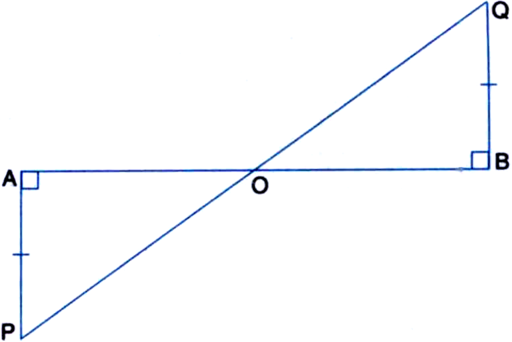
In figure, AP and BQ are perpendiculars to the line-segment AB and AP = BQ. Prove that O is the midpoint of line segments AB and PQ.