Circles
ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF. Prove that ED and FC are perpendicular to each other.
Given: ABCD is a rhombus and AB is produced to E and F such that AE = AB = BF.
To Prove: ED ⊥ FC.
Proof: AB = BF | By construction
AB = BC
| ∵ ABCD is a rhombus
∴ BC = BF
∴ ∠1 = ∠2 ...(1)
| Angles opposite to equal sides of a ∆ are equal
In ∆BCF,
Ext. ∠3 = ∠1 + ∠2 = ∠1 + ∠1
| From(1)
= 2 ∠1 ...(2)
AB = AE | By construction
AB = AD
| ∵ ABCD is a rhombus
∴ AD = AE
∴ ∠5 = ∠6 ...(3)
| Angles opposite to equal sides of a ∆ are equal
In ∆ADE,
Ext. ∠4 = ∠5 + ∠6 = ∠5 + ∠5
| From (3)
= 2 ∠5 ...(4)
∵ AD || BC
and transversal AB intersects them
∴ ∠3 + ∠4 = 180°
| ∵ Consecutive interior angles on the same side of a transversal are supplementary
⇒ 2∠1 + 2∠5 = 180° | From (2) and (4)
⇒ ∠1 + ∠5 = 90° ...(5)
In ∆GEF,
∠1 + ∠5 + ∠EGF = 180°
| ∵ The sum of the three angles of a ∆ is 180°
⇒ 90° + ∠EGF = 180° | From (5)
⇒ ∠EGF = 90°
⇒ EG ⊥ GF
⇒ ED ≁ FC.
Sponsor Area
Some More Questions From Circles Chapter
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Show that the diagonals of a square are equal and bisect each other at right angles.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that:
(i) it bisects ∠C also
(ii) ABCD is a rhombus.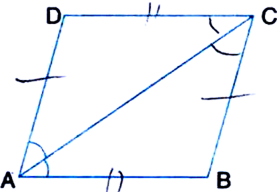
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see figure). Show that:
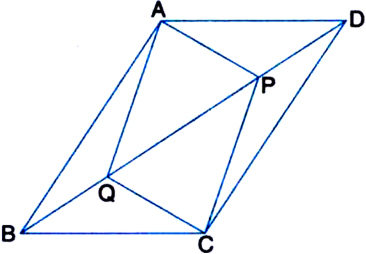
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) APCQ is a parallelogram.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD respectively (see figure). Show that:
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.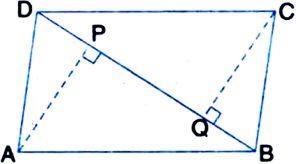
In ∆ABC and ∆DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, Band C are joined to vertices D, E and F respectively (see figure). Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram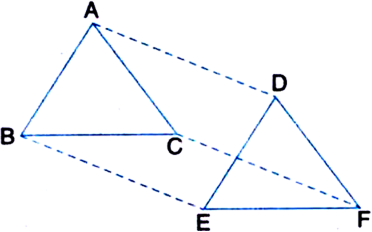
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF. [CBSE 2012
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area