Quadrilaterals
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
(i) It is given that AB = DE and AB || DE.
If two opposite sides of a quadrilateral are equal and parallel to each other, then it will be a parallelogram.
Therefore, quadrilateral ABED is a parallelogram.
(ii) Again, BC = EF and BC || EF
Therefore, quadrilateral BCEF is a parallelogram.
(iii) As we had observed that ABED and BEFC are parallelograms, therefore
AD = BE and AD || BE
(Opposite sides of a parallelogram are equal and parallel)
And, BE = CF and BE || CF
(Opposite sides of a parallelogram are equal and parallel)
∴ AD = CF and AD || CF
(iv) As we had observed that one pair of opposite sides (AD and CF) of quadrilateral ACFD are equal and parallel to each other, therefore, it is a parallelogram.
(v) As ACFD is a parallelogram, therefore, the pair of opposite sides will be equal and parallel to each other.
∴ AC || DF and AC = DF
(vi) ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (ACFD is a parallelogram)
∴ ΔABC ≅ ΔDEF (By SSS congruence rule)
Sponsor Area
Some More Questions From Quadrilaterals Chapter
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that
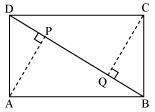
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that
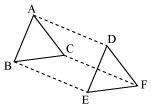
(i) Quadrilateral ABED is a parallelogram
(ii) Quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) Quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that
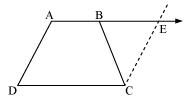
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid – point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
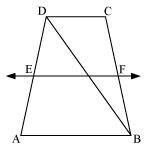
Mock Test Series
Sponsor Area
NCERT Book Store
NCERT Sample Papers
Sponsor Area