The angles of quadrilateral are in the ratio 3: 5: 9: 13.

Find all the angles of the quadrilateral.

ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (See the given figure). Show that

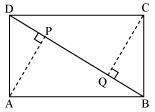
(i) ΔAPB ≅ ΔCQD

(ii) AP = CQ

In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see the given figure). Show that

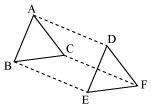
(i) Quadrilateral ABED is a parallelogram

(ii) Quadrilateral BEFC is a parallelogram

(iii) AD || CF and AD = CF

(iv) Quadrilateral ACFD is a parallelogram

(v) AC = DF

(vi) ΔABC ≅ ΔDEF.

ABCD is a trapezium in which AB || CD and AD = BC (see the given figure). Show that

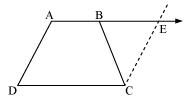
(i) ∠A = ∠B

(ii) ∠C = ∠D

(iii) ΔABC ≅ ΔBAD

(iv) diagonal AC = diagonal BD

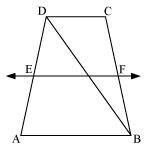
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid – point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.