एक पेटी में 12 गेंदे हैं, जिनमें से x गेंद काली है। यदि इसमें से एक गेंद यादृच्छया निकाली जाती है, तो इसकी प्रायिकता ज्ञात कीजिए की यह गेंद काली है।
यदि इस पेटी में 6 काली गेंद और डाल दी जाएँ, तो काली गेंद निकालने की प्रायिकता पहेली प्रायिकता की दुगुनी हो जाती है। x का मान ज्ञात कीजिए।

Solution

(i) थैले में गेंदों की कुल संख्या = 12
अत: सभी संभव परिणामों की संख्या = 12
काली गेंदों की संख्या = x
अर्थात् अनुकूल परिणामों की संख्या = x
अब, P(एक काली गेंद) = $fraction numerator अन ु क ू ल space पर ि ण ा म ों space क ी space स ं ख ् य ा space over denominator सभ ी space स ं भव space पर ि ण ा म ों space क ी space क ु ल space स ं ख ् य ा space end fraction$
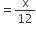
$equals straight x over 12$
(ii) क्योंकि थैले में 6 काली गेंदे और रख दी गई हैं।
∴ थैले में गेंदों की कुल संख्या = 12 + 6 = 18
थैले में काली गेंदों की कुल संख्या = 6 + x
∴ सभी संभव परिणामों की कुल संख्या = 18
अनुकूल परिणामों की संख्या = 6 + x
∴ P(काली गेंद) = 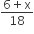$fraction numerator 6 plus straight x over denominator 18 end fraction$
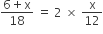
प्रश्नानुसार, $fraction numerator 6 plus straight x over denominator 18 end fraction space equals space 2 space cross times space straight x over 12$
या $fraction numerator 6 plus straight x over denominator 18 end fraction equals straight x over 6$
या $6 left parenthesis 6 plus straight x right parenthesis space equals space 18 straight x$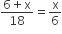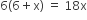
या 36 + 6x = 18x
या 18x = 36 + 6x
या 18x - 6x = 36
या 12x = 36
या 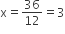$straight x equals 36 over 12 equals 3$
अत: x = 3