Sponsor Area
त्रिकोणमितीय सर्वसमिकाएँ
Question
भूमि के एक बिंदु से, जो मीनार के पाद -बिंदु से 30m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 
है। मीनार की ऊँचाई ज्ञात कीजिए।
Solution
माना मीनार AB का शिखर A तथा पाद-बिंदु B है जिसकी ऊँचाई h m है। बिंदु C मीनार के पाद-बिंदु B से 30m की दूरी पर है।
अब,
AB = h m
BC = 30 m
and 
= 30°
समकोण 
में,
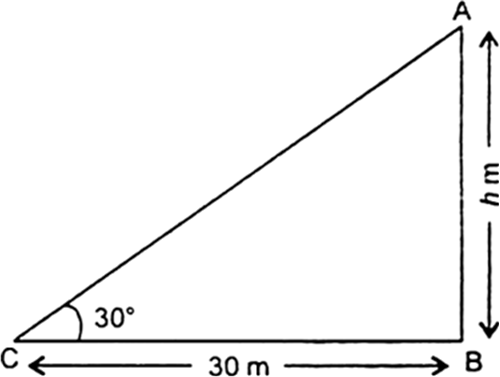
अत: मीनार की ऊँचाई (AB) = 
Some More Questions From त्रिकोणमितीय सर्वसमिकाएँ Chapter
Sponsor Area
Mock Test Series
Mock Test Series