Question
A proton and an α-particle have the same de-Broglie wavelength. Determine the ratio of
(i) their accelerating potentials
(ii) their speeds.
Solution
De-broglie wavelength of the particle is given by, 
;
where, V= Accelerating potential and v is the speed of the particle.
Given that, the de-broglie wavelength is same for both proton and a-particle.
Charge on 
particle = 2 qp;
Mass of 
-particle = 4 mp
Charge on proton= qp ;
Mass of proton = mp 
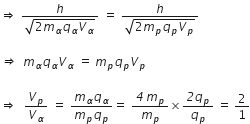
2 : 1 is the required ratio of the accelerating potential.
Also,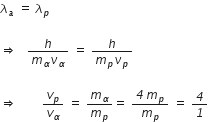 
4 : 1 is the required ratio of the speed of proton to speed of alpha-particle.
