Sponsor Area
Wave Optics
Question
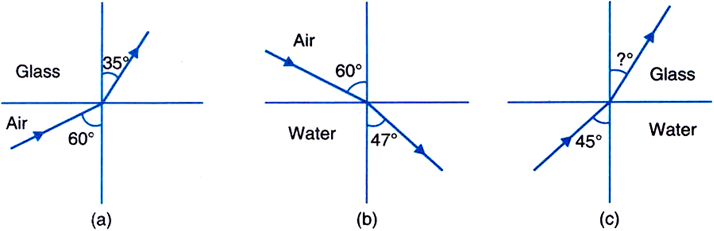
Figures (a) and (b) show refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45° with the normal to a water-glass interface. [ Fig. 9.34 (c)].
Solution
(a)
Given,
Using Snell's law, we have
Refractive index of glass with respect to air,
(b)
Using Snell's law,
Refractive index of water wr.to air,
(c)
Angle of incidence in water,
Refractive index of glass wr.to water,
Some More Questions From Wave Optics Chapter
Sponsor Area
Mock Test Series
Mock Test Series





