An emf V_o sin ωt is applied to a circuit which consists of a self-inductance L of negligible resistance in series with a variable capacitor C. The capacitor is shunted by a variable resistance R. Find the value of C for which the amplitude of the current is independent of R.

Solution

Let us make use of phasor algebra to make the problem a little easier.
The complex impedance, of the circuit as shown in the figure.

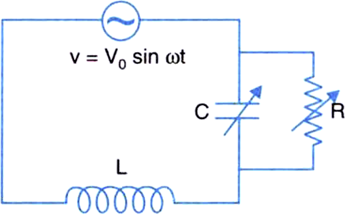
Impedence,

Z = jωL + Z'

where Z' is complex impedance due to C and R in parallel and is given by

\frac{1}{Z'} = \frac{1}{R} + jωC = \frac{1 + jωCR}{R}

Z' = \frac{R}{1 + jωCR} = \frac{R (1 - jωCR)}{1 + ω^{2} C^{2} R^{2}}

∴

Z = jωL + \frac{R (1 - jωCR)}{1 + ω^{2} C^{2} R^{2}}

= \frac{R}{1 + ω^{2} C^{2} R^{2}} + j (ωL - \frac{{ωCR}^{2}}{1 + ω^{2} C^{2} R^{2}})

The magnitude of Z is thus given by,

Z = \sqrt{[\frac{R^{2}}{(1 + ω^{2} C^{2} R^{2})^{2}} + {(ωL - \frac{{ωCR}^{2}}{1 + ω^{2} C^{2} R^{2}})}^{2}]}

Z^{2} = \frac{R^{2}}{{(1 + ω^{2} C^{2} R^{2})}^{2}} + ω^{2} L^{2} + \frac{ω^{2} C^{2} R^{4}}{(1 + ω^{2} C^{2} R^{2})^{2}} - \frac{2 ω^{2} {LCR}^{2}}{1 + ω^{2} C^{2} R^{2}}

= \frac{R^{2} - 2 ω^{2} {LCR}^{2}}{1 + ω^{2} C^{2} R^{2}} + ω^{2} L^{2}

The peak value of current will be independent of R, if Z or Z² is also independent of R.

It is possible when

R^{2} - 2 ω^{2} {LCR}^{2} = 0, or C = \frac{1}{2 ω^{2} L}

For Daily Free Study Material Join wiredfaculty