Prove that the current density of a metallic conductor is directly proportional to the drift speed of electrons.

Consider,  a conductor of length l and area of cross-section A having n electrons per unit length, as shown in the figure.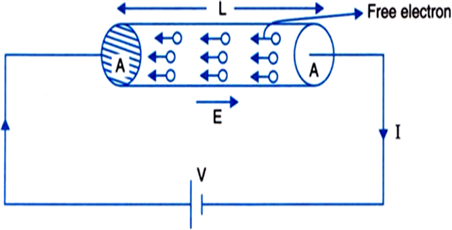 



Volume of the conductor , V = Al 
∴ Total number of electrons in the Conductor = Volume x electron density = Al x n .

If e is the charge of an electron, then total charge contained in the conductor, Q = en.Al 

Electric field in the conductor when potential difference V is applied across the conductor, E= V/I

Under the influence of this field E, free electrons begin to drift in a direction opposite to that of the direction of field.
Time taken by electrons to cross-over the conductor is
                     $\mathrm{t} = \frac{\mathrm{l}}{{\mathrm{\nu }}_{\mathrm{d}}}$
where, v_d is the drift velocity of electrons.
Therefore, current flowing through the conductor is given by 

               $\mathrm{I} = \frac{\mathrm{Q}}{\mathrm{t}} = \frac{\mathrm{en} \mathrm{Al}}{\mathrm{l}/{\mathrm{\nu }}_{\mathrm{d}}}$ 

$\Rightarrow$           $$\begin{gathered} \mathrm{I} = \mathrm{ne} \mathrm{A} {\mathrm{\nu }}_{\mathrm{d}} \\ \frac{\mathrm{I}}{\mathrm{A}} = {\mathrm{n}}_{\mathrm{e}}{\mathrm{v}}_{\mathrm{d}} \end{gathered}$$
$\Rightarrow$            $\mathrm{I} \mathrm{\alpha } {\mathrm{\nu }}_{\mathrm{d}}$   [$\because$ n, e A are all constant] 

Thus, current density is proportional to drift velocity.