A 0.5 m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15 T. If the resistance of the total circuit is 3 Ω, calculate the force needed to move the rod in the direction as indicated with a constant speed of 2 m s^–1.

 

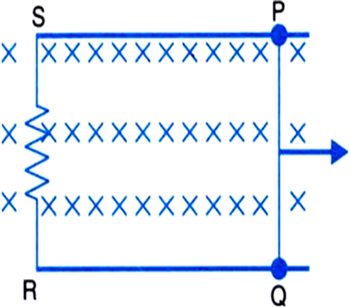
Length of the metal rod PQ, l = 0.5 m
Magnetic field, B = 0.15 T
Resistance of the circuit, R = 3 Ω 

Consider coil PQRS with its arm PQ movable as shown in the figure.
A magnetic field is applied normal to the surface of the coil.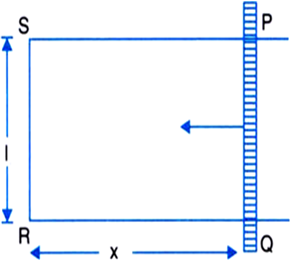


Area of the coil, ΔS = l x (x) and,
Flux, Φ = 8 Δ S = Blx 

The rate of change of magnetic flux linked with the coil is given by 

                   $$\begin{gathered} \frac{\mathrm{d\varphi }}{\mathrm{dt}} = \frac{\mathrm{d}\left(\mathrm{Blx}\right)}{\mathrm{dt}} \\ = \mathrm{Bl}\frac{\mathrm{dx}}{\mathrm{dt}} \\ =\mathrm{Blv} \end{gathered}$$
If e is the induced emf produced, then 

$\mathrm{e} =-\frac{\mathrm{d\varphi }}{\mathrm{dt}} = \mathrm{Blv}$ $\left[\because \mathrm{x} \mathrm{is} \mathrm{decreasing}, \frac{\mathrm{d}\left(\mathrm{x}\right)}{\mathrm{dt}} \mathrm{is} - \mathrm{Ve}\right]$ 

Let R be the resistance of movable arm PQ of the rectangular conductor. Taking the resistance of other arms as negligibly small, the current in the loop is given by, 
              I = $\frac{\mathrm{\epsilon }}{\mathrm{R}} =\frac{\mathrm{Blv}}{\mathrm{R}}$                     ...(I) 
The arm PQ moves with the speed v.
The power required to move it is given by, 

                            $\mathrm{F} = \mathrm{BIL}$ 

$\therefore$                        $\mathrm{F} = \frac{{\mathrm{Bl}}^2\mathrm{v}}{\mathrm{R}}$              (From I)
$\Rightarrow$           $\mathrm{F} = \frac{{\mathrm{B}}^2{\mathrm{l}}^2\mathrm{v}}{\mathrm{R}} = \frac{(0.15) (0.5{)}^2 2 }{3}$
                              $= 3.75 \times {10}^{-3}\mathrm{N}.$