Magnetism And Matter

Question

Wired Faculty App

If δ₁ and δ₂ be the angles of dip observed in two planes at right angles to each other and δ is the true angle of dip, then prove that
cot² δ₁ + cot² δ₂ = cot² δ

Solution

Given, δ₁ and δ₂are the angles of dip right angle to each other in planes.
δ is the true angle of dip.

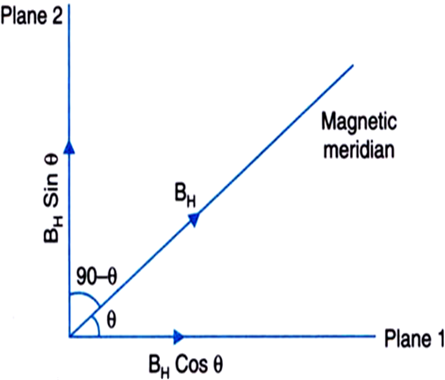
If horizontal and vertical components of earth's magnetic field are represented by B_Hand B_v respectively, then

\tan δ = \frac{B_{V}}{B_{H}}

Let, δ₁ be the (apparent) dip in a plane which makes angle θ with the magnetic meridian.
In this plane, the vertical component will be B_V only but the effective horizontal component will be B_H cos θ.

Therefore,

\tan δ = \frac{B_{V}}{B_{H} \cos θ}

\tan δ_{1} = \frac{\tan δ}{\cos θ}

[

∵

B_{V} = B_{H} tanδ

]

\cos θ = \frac{\tan δ}{\tan δ_{1}} = \tan \cot δ_{1}

...(i)

Let, δ₂ be the (apparent) dip in the second plane.
The angle made by this plane with the magnetic meridian will be (90° – θ).
Effective horizontal component in this plane is B_H cos (90° – θ) i.e., B_H sin θ.

The vertical component will be B_v only.
   $\tan δ_{2} = \frac{B_{V}}{B_{H} \sin θ} = \frac{\tan δ}{\sin θ}$

   $\sin θ = \frac{\tan δ}{\tan δ_{2}} = tanδ \cot δ_{2}$ ...(ii)

Squaring and adding equation (i) and (ii), we get
   $\cos^{2} θ + \sin^{2} θ = \tan^{2} δ \cot^{2} δ_{1} + \tan^{2} δ \cot^{2} δ_{2}$

   $1 = \tan^{2} δ (\cot^{2} δ_{1} + \cot^{2} δ_{2})$

$\cot^{2} δ = \cot^{2} δ_{1} + \cot^{2} δ_{2}$

Hence proved.

Some More Questions From Magnetism and Matter Chapter

Answer the following question regarding earth:
Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth's surface oriented in different directions. How is such a thing possible at all?

Answer the following question:
The earth's magnetic field varies from point to point in space. Does it also change with time? If so, on what time scale does it change appreciably?

Answer the following question:
The earth's core is known to contain iron. Yet geologists do not regard this as a source of the earth's magnetism. Why?

Answer the following question:
The charged currents in the outer conducting regions of the earth's core are thought to be responsible for earth's magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?

Answer the following question:
The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth's field in such distant past?

Answer the following question:
The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?

For Daily Free Study Material Join wiredfaculty

Magnetism And Matter

If δ₁ and δ₂ be the angles of dip observed in two planes at right angles to each other and δ is the true angle of dip, then prove that
cot² δ₁ + cot² δ₂ = cot² δ

Some More Questions From Magnetism and Matter Chapter

Answer the following question regarding earth:
Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth's surface oriented in different directions. How is such a thing possible at all?

Answer the following question:
The earth's magnetic field varies from point to point in space. Does it also change with time? If so, on what time scale does it change appreciably?

Answer the following question:
The earth's core is known to contain iron. Yet geologists do not regard this as a source of the earth's magnetism. Why?

Answer the following question:
The charged currents in the outer conducting regions of the earth's core are thought to be responsible for earth's magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?

Answer the following question:
The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth's field in such distant past?

Answer the following question:
The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Magnetism And Matter

If δ1 and δ2 be the angles of dip observed in two planes at right angles to each other and δ is the true angle of dip, then prove thatcot2 δ1 + cot2 δ2 = cot2 δ

Some More Questions From Magnetism and Matter Chapter

Answer the following question regarding earth:Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth's surface oriented in different directions. How is such a thing possible at all?

Answer the following question:The earth's magnetic field varies from point to point in space. Does it also change with time? If so, on what time scale does it change appreciably?

Answer the following question:The earth's core is known to contain iron. Yet geologists do not regard this as a source of the earth's magnetism. Why?

Answer the following question:The charged currents in the outer conducting regions of the earth's core are thought to be responsible for earth's magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?

Answer the following question:The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth's field in such distant past?

Answer the following question:The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

If δ₁ and δ₂ be the angles of dip observed in two planes at right angles to each other and δ is the true angle of dip, then prove that
cot² δ₁ + cot² δ₂ = cot² δ

Answer the following question regarding earth:
Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth's surface oriented in different directions. How is such a thing possible at all?

Answer the following question:
The earth's magnetic field varies from point to point in space. Does it also change with time? If so, on what time scale does it change appreciably?

Answer the following question:
The earth's core is known to contain iron. Yet geologists do not regard this as a source of the earth's magnetism. Why?

Answer the following question:
The charged currents in the outer conducting regions of the earth's core are thought to be responsible for earth's magnetism. What might be the ‘battery’ (i.e., the source of energy) to sustain these currents?

Answer the following question:
The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth's field in such distant past?

Answer the following question:
The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?