Question

Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

Solution

Let, the charge possessed by two conducting spheres of radii a and b be q₁and q₂respectively.

Potential on the surface of first sphere, V₁=

\frac{1}{4 {πε}_{0}} . \frac{q_{1}}{a}

Potential on the surface of second sphere, V₂=

\frac{1}{4 {πε}_{0}} . \frac{q_{2}}{b}

Till the potentials of two conductors become equal the flow of charges continue.

V_{1} = V_{2}

\Rightarrow

\frac{1}{4 {πε}_{0}} . \frac{q_{1}}{a} = \frac{1}{4 {πε}_{0}} . \frac{q_{2}}{b}

\Rightarrow

\frac{q_{1}}{q_{2}} = \frac{a}{b}

Now,
Electric field on sphere 1, E₁=

\frac{1}{4 {πε}_{0}} . \frac{q_{1}}{a^{2}}

Electric field on sphere 2, E₂=

\frac{1}{4 {πε}_{0}} . \frac{q_{2}}{b^{2}}

\Rightarrow

\frac{E_{1}}{E_{2}} = \frac{q_{1}}{q_{2}} . \frac{b^{2}}{a^{2}} = \frac{a}{b} . \frac{b^{2}}{a^{2}} = \frac{b}{a}

Therefore, the ratio of the electric field of first sphere to that of the second sphere is b:a.

The surface charge densities of the two spheres are given as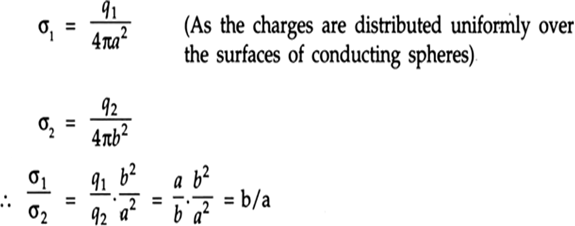

This implies,
The surface charge densities are inversely proportional to the radii of the sphere.
The surface charge density on the sharp and pointed ends of a conductor is higher than on its flatter portion since a flat portion may be taken as a spherical surface of large radius and a pointed portion as that of small radius.

For Daily Free Study Material Join wiredfaculty

Electrostatic Potential And Capacitance

Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

Some More Questions From Electrostatic Potential and Capacitance Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction