Question
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Solution
Given,
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, v = 20 cm/s = 0.2 m/s
Total energy of the hoop = Translational K.E. + Rotational K.E.
ET =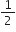 mv2 +
mv2 + 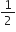 I ω2
I ω2
Moment of inertia of the hoop about its centre, I = mr2
ET =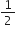 mv2 +
mv2 +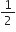 (mr2)ω2
(mr2)ω2
Using the relation, v = rω
∴ ET =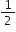 mv2 +
mv2 + 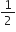 mr2ω2
mr2ω2
=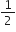 mv2 +
mv2 +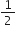 mv2
mv2
= mv2
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
∴ Required work to be done, W = mv2
= 100 × (0.2)2
= 4 J.
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, v = 20 cm/s = 0.2 m/s
Total energy of the hoop = Translational K.E. + Rotational K.E.
ET =
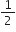 mv2 +
mv2 + 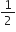 I ω2
I ω2Moment of inertia of the hoop about its centre, I = mr2
ET =
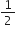 mv2 +
mv2 +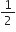 (mr2)ω2
(mr2)ω2 Using the relation, v = rω
∴ ET =
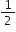 mv2 +
mv2 + 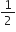 mr2ω2
mr2ω2 =
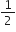 mv2 +
mv2 +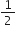 mv2
mv2 = mv2
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
∴ Required work to be done, W = mv2
= 100 × (0.2)2
= 4 J.



