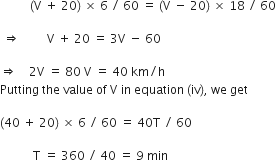Question
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h-1 in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
Solution
Let V be the speed of the bus running between towns A and B.
Given,
Speed of the cyclist = 20 km/hr
Relative speed of bus moving in the direction of the cyclist = V - v = (V-20) km/hr
Every 18 mins, the bus went past the cyclist. moving in the direction of the bus.
That is,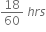 
Distance covered by the bus =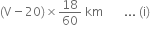 
One bus leaves every t minutes.
Therefore,
Distance travelled by the bus = V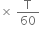 
... (ii)
Equations (i) and (ii) are equal.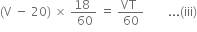 
Relative speed of the bus moving in the opposite direction of the cyclist = (V + 20) km/h
Time taken by the bus to go past the cyclist = 6 min = 6 / 60 h
Therefore,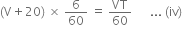 
Now, from equations (3) and (4), we get
