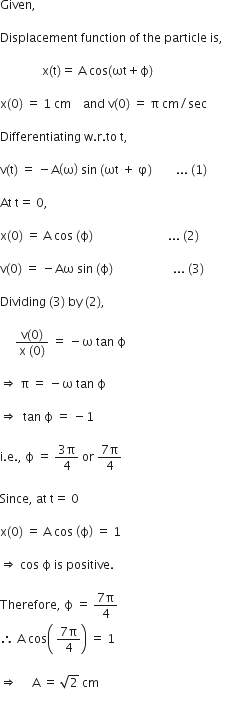Question
A particle in simple harmonic motion is described by displacement function x(t) = A cos(ωt + ϕ) If the initial position of the particle is 1cm and initial velocity is π cm/s, then what is its amplitude and initial phase? Let angular frequency of particle be π per second.
Solution