Derive an expression for excess of pressure inside a soap bubble.

Consider a soap bubble of radius R and surface tension T.
There are two free surfaces of soap bubble. Due to surface tension the molecules on the surface film experience the net force in inward direction normal to the surface.
Therefore there is more pressure inside than outside.
Let p_i be pressure inside the liquid drop and p_o the pressure outside the drop.
Therefore excess of pressure inside the liquid drop is,

                     p =p₁–P_o

Due to excess of pressure inside the liquid drop, the free surface of the drop will experience the net force in outward direction due to which the drop expands.
Let the free surface be displaced by dR under isothermal conditions.

Therefore excess of pressure does the work in displacing the surface and that work will be stored in the form of potential energy.

The work done by excess of pressure in displacing the surface is,
dW= Force x displacement 
     = (excess of pressure x Surface area) x displacement of surface
     
Increase in the potential energy is given by, 
dU = surface tension x increase in area of the free surface
   
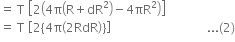
From (1) and (2)
   
p is the excess of pressure inside a soap bubble.