A 5 cm tall object is placed perpendicular to the principle axis of a convex lens of focal length 12 cm. The distance of the object from the lens is 8 cm. Using the lens formula, find the position, size and nature of the image formed.

Given,
Object distance from the lens, u = - 8 cm
Focal length of the lens, f = 12 cm
Height of the object, h = 5 cm
Using the lens formula,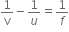

Putting the values,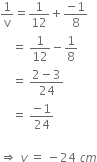

Thus, image is formed 24 cm on the left of the convex lens.
That is, object is formed on the same side of the object.
Now,
Magnification, m =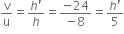 
That is,
Height of the image, h' = 15 cm (positive)
Height of the image is 15 cm which is 3 times larger than the height of the object.
Therefore, the image formed is virtual, enlarged and erect.