By stating the sign-convention and assumptions used, derive the relation between object distance u, image distance v and focal length f for a thin convex lens, when it forms real image of an object of finite size.

The refraction of light through spherical lenses follows new cartesian sign convention: 

According to this sign convention: 

(i) All distances are measured from the optical centre of the lens.

(ii) The distances measured in the same direction as the incident light are taken positive.

(iii) The distances measured in the direction opposite to the direction of incident light are taken negative.

(iv) Heights measured upwards and perpendicular to the principal axis are taken positive.

(v) Heights measured downwards and perpendicular to the principal axis are taken negative.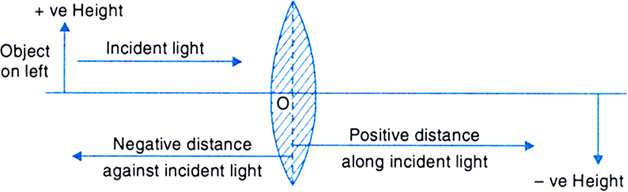



Assumptions used in the derivation of lens formula:

(i) The lens used is thin. 

(ii) The aperture of the lens is small. 

(iii) The incident and refracted rays make small angles with the principal axis. 

(iv) The object is a small object placed on the principal axis. 

Derivation of lens formula for a convex lens.

As shown in Fig, consider an object AB placed perpendicular to the principal axis of a thin convex lens between its F₁ and 2F₁.
A real, inverted and magnified image AB' is formed beyond 2F₂ on the other side of the lens.


Fig. Real image formed by a convex lens.


$∆\mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{O} \mathrm{and} ∆ \mathrm{ABO} \mathrm{are} \mathrm{similar},$ 

$\therefore$       $\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}} = \frac{\mathrm{OB}\text{'}}{\mathrm{BO}}$                                 ...(1) 

Also,  $∆ \mathrm{A}\text{'}\mathrm{B}\text{'}\mathrm{F} \mathrm{and} ∆ \mathrm{MOF}$  are similar, 

$\therefore$      $\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{MO}} = \frac{\mathrm{FB}\text{'}}{\mathrm{OF}}$ 

But MO = AB, 

$\therefore$     $\frac{\mathrm{A}\text{'}\mathrm{B}\text{'}}{\mathrm{AB}} = \frac{\mathrm{FB}\text{'}}{\mathrm{OF}}$                                    ...(2) 


From (1) and (2), we get    

$\frac{\mathrm{OB}\text{'}}{\mathrm{BO}} =\frac{\mathrm{FB}\text{'}}{\mathrm{OF}} = \frac{\mathrm{OB}\text{'} - \mathrm{OF}}{\mathrm{OF}}$ 

Using new Cartesian sign convention, we get 

Object distance,    BO = -u
Image distance, OB' = +v
Focal length, OF₂ = + f 

$\therefore$            $\frac{\mathrm{v}}{-\mathrm{u}} = \frac{\mathrm{v}-\mathrm{f}}{\mathrm{f}}$  

$\Rightarrow$               $\mathrm{vf} = -\mathrm{uv} + \mathrm{uf}$ 

$\Rightarrow$              $\mathrm{uv} = \mathrm{uf} - \mathrm{vf}$ 

Dividing both sides by uvf, we get 

                 $\frac{1}{\mathrm{f}} = \frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}$ 

This proves the lens formula for a convex lens.