Question
A line with direction cosines proportional to 2, 1, 2 meets each of the lines x = y + a = z and x + a = 2y = 2z. The co-ordinates of each of the point of intersection are given by
-
(3a, 3a, 3a), (a, a, a)
-
(3a, 2a, 3a), (a, a, a)
-
(3a, 2a, 3a), (a, a, 2a)
-
(2a, 3a, 3a), (2a, a, a)
Solution
B.
(3a, 2a, 3a), (a, a, a)
Any point on the line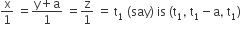 
and any point on the line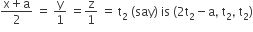 
Now direction cosine of the lines intersecting the above lines is proportional to (2t2 – a – t1, t2 – t1 + a, t2 – t1).
Hence 2t2 – a – t1 = 2k , t2 – t1 + a = k and t2 – t1 = 2k
On solving these, we get t1 = 3a , t2 = a. Hence points are (3a, 2a, 3a) and (a, a, a).
