Find the volume of the largest cylinder that can be inscribed in a sphere of radius r.

Solution

The given sphere is of radius R. Let h be the height and r be the radius of the cylinder inscribed in the sphere.

Volume of cylinder

$V = {πR}^{2} h . . . . . . . . . (i)$

In right angled triangle $∆ OBA$

${AB}^{2} + {OB}^{2} = {OA}^{2} R^{2} + \frac{h^{2}}{4} = r^{2} So, R^{2} = r^{2} - \frac{h^{2}}{4} . . . . . . . . . . . . . (ii)$

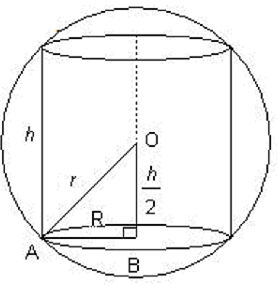
Putting the value of R² in equation (i), we get

$V = π (r^{2} - \frac{h^{2}}{4}) . h V = π (r^{2} h - \frac{h^{3}}{4}) . . . . . . . . . . . . . . . (iii) ∴ \frac{dV}{dh} = π (r^{2} - \frac{3 h^{2}}{4}) . . . . . . . . . . . . . . . (iv) For stationary point, \frac{dV}{dh} = 0 π (r^{2} - \frac{3 h^{2}}{4}) = 0 r^{2} = \frac{3 h^{2}}{4} \Rightarrow h^{2} = \frac{4 r^{2}}{3} \Rightarrow h = \frac{2 r}{\sqrt{3}} Now \frac{d^{2} V}{{dh}^{2}} = π (- \frac{6}{4} h) ∴ {[\frac{d^{2} V}{{dh}^{2}}]}_{at h - \frac{2 r}{\sqrt{3}}} = π (- \frac{3}{2} . \frac{2 r}{\sqrt{3}}) < 0$

$∴ Volume is maximum at h = \frac{2 r}{\sqrt{3}} Maximum volume is = π (r^{2} x \frac{2 r}{\sqrt{3}} - \frac{1}{4} x \frac{8 r^{3}}{3 \sqrt{3}}) = π (\frac{2 r^{3}}{\sqrt{3}} - \frac{2 r^{3}}{3 \sqrt{3}}) = π (\frac{6 r^{3} - 2 r^{3}}{3 \sqrt{3}}) = \frac{4 {πr}^{3}}{3 \sqrt{3}} cu . unit$

For Daily Free Study Material Join wiredfaculty

Application Of Derivatives

Find the volume of the largest cylinder that can be inscribed in a sphere of radius r.

Some More Questions From Application of Derivatives Chapter

The radius of a circle is increasing uniformly at the rate of 4 cm per second Find the rate at which the area of the circle is increasing when the radius is 8 cm.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction