Question
Find the intervals in which the function f given by is
(i) increasing
(ii) decreasing.
Solution
(i) For an increasing function, we should have,
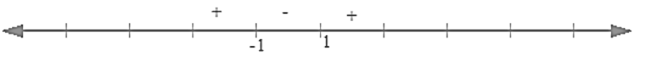
So, f( x ) is increasing on
(ii) For a decreasing function, we should have f ( x ) 0
![]()
So, f ( x ) is decreasing on ( -1, 0 ) ( 0, 1 )



