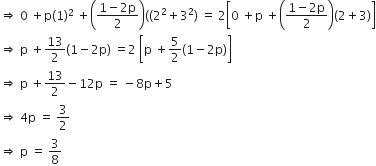Question
The random variable X can take only the values 0, 1, 2, 3. Given that P(X =0) = P(X = 1) = p and P(X = 2) = P(X = 3) such that Σpixi2 = 2Σpixi, find the value of p.
Solution
It is given that the random variable X can take only the values 0,1,2,3.
Given:
P(X = 0) = P( X =1) =p
P(X =2) =P(X =3)
Let P (X =2) = P(X =3) =q
Now,
P(X =0) + P(X =1) +P(X =2) +P(X =3) =1
⇒ p +p+(q+q) = 1
since Σpixi2 = 2Σpixi,