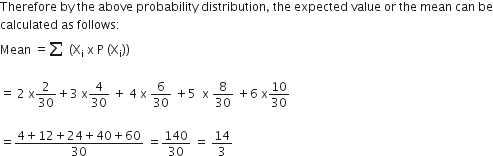Three numbers are selected at random (without replacement) from first six positive integers. Let X denote the largest of the three numbers obtained. Find the probability distribution of X.Also, find the mean and variance of the distribution.
The first six positive integers are 1, 2, 3, 4, 5, 6.
We can select the two positive numbers in 6 × 5 = 30 different ways.
Out of this, 2 numbers are selected at random and let X denote the larger of the two numbers.
Since X is large of the two numbers, X can assume the value of 2, 3, 4, 5 or 6.
P (X =2) = P (larger number is 2) = {(1,2) and (2,1)} = 2/1
P (X = 3) = P (larger number is 3) = {(1,3), (3,1), (2,3), (3,2)} =4/3
P (X = 4) = P (larger number is 4) = {(1,4), (4,1), (2,4), (4,2), (3,4), (4,3)} = 6/30
P (X = 5) = P (larger number is 5) = {(1,5), (51,), (2,5), (5,2), (3,5), (5,3), (4,5), (5.4)} = 8/30
P (X = 6) = P (larger number is 6) = {(1,6), (6,1), (2,6), (6,2), (3,6), (6,3), (4,6), (6,4), (5,6), (6,5)} = 10/30