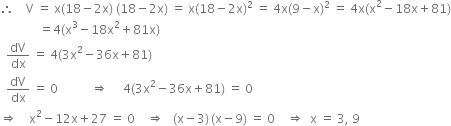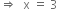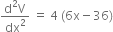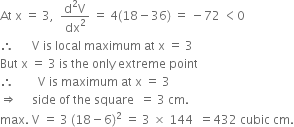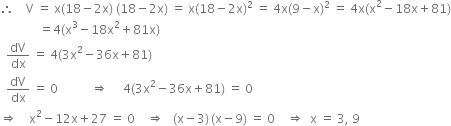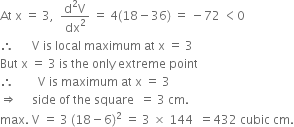Question
A square piece of a tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form a box. What should be the side of the square to be cut off, so that the volume of the box is the maximum possible?
Solution
Let x (0 < x < 9) cm be the length of each side of the square which is to be cut from corners of the square tin sheet of each side 18 cm. Let V be the volume of the box formed by folding up the flaps.