Question
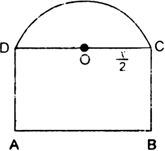
A window consists of a semi-circle with a rectangle on its diameter. If the perimeter of the window is 30 metres, find the dimensions of the window in order that its area may be maximum.
Or
A window is in the form of a rectangle surmounted by a semi-circle. If the total perimeter of the window is 30 m. find the dimensions of the window so that maximum light is admitted.
Solution
Let x, y be length, breadth of the rectangle ABCD. Let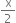 
be the radius of semi-circle with centre at O.
Let P be the perimeter of figure.
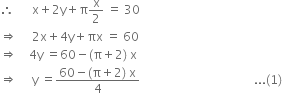
Let A be area of the figure.
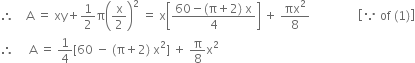
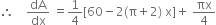
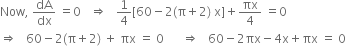
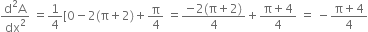
When
and
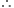area of figure is maximum i.e. maximum light is admitted when length of rectangle =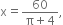 
breadth of rectangle
radius of semi-circle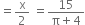
be the radius of semi-circle with centre at O.Let P be the perimeter of figure.
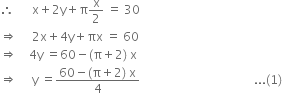
Let A be area of the figure.
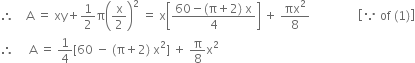
When
and
area of figure is maximum i.e. maximum light is admitted when length of rectangle = breadth of rectangle
radius of semi-circle
