A wire of length 36 cm is cut into two pieces. One of the pieces is turned in the form of a square and the other in the form of an equilateral triangle. Find the length of each piece so that the sum of the areas of the two be minimum.
Total length of wire = 36 cm
Let x cm be length of each side of square and y cm be length of each side of quilateral triangle.
Length of wire used for square = 4x cms
and length of wire used for triangle = 3y cms
∴ 4x + 3y = 36 ⇒ 3y = 36 – 4x![]() ...(1)
...(1)
Let A denote the sum of the areas of square and equilateral triangle.![]()
![]()
![]()
![]()
![]()
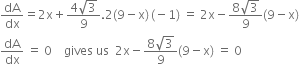
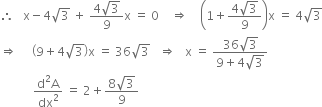
![]()
![]()
Length of piece required for square = 4x = ![]()
and length of piece required for triangle = 3y = 36 - 4x
![]()



