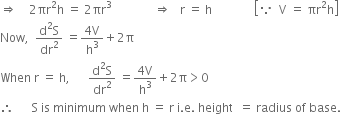+91-8076753736 [email protected]

-->

Application Of Derivatives

Question

Wired Faculty App

Show that a cylinder of given volume open at the top has minimum total surface area provided its height is equal to the radius of its base.

Solution

Let r be the radius of base of circular cylinder and h be its height. Let V be volume and S be the total surface area.

therefore space space space straight V space equals space πr squared straight h space space space space space space space space space space space space space space space rightwards double arrow space space space space straight h space equals space straight V over πr squared

...(1)
Also,

straight S space equals 2 πrh plus πr squared

open square brackets because space cylinder space is space open space at space top close square brackets

equals 2 πr. space straight V over πr squared plus πr squared

open square brackets because space of space left parenthesis 1 right parenthesis close square brackets

therefore space space space space straight S space space equals fraction numerator 2 straight V over denominator straight r end fraction plus πr squared space space space space space space space space space space space space space rightwards double arrow space space space dS over dr space equals negative fraction numerator 2 straight V over denominator straight r squared end fraction plus 2 πr

Now,

dS over dr space equals 0 space space space space space rightwards double arrow space space space minus fraction numerator 2 straight V over denominator straight r squared end fraction plus 2 πr space equals space 0 space space space space rightwards double arrow space space space space 2 straight V space equals space 2 πr cubed

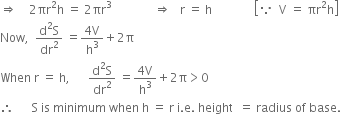
rightwards double arrow space space space space 2 πr squared straight h space equals space 2 πr cubed space space space space space space space space space space space space space space rightwards double arrow space space space straight r space equals space straight h space space space space space space space space space space space space space space open square brackets because space space straight V space equals space πr squared straight h close square brackets Now comma space space fraction numerator straight d squared straight S over denominator dr squared end fraction space equals fraction numerator 4 straight V over denominator straight h cubed end fraction plus 2 straight pi When space straight r space equals space straight h comma space space space space space space fraction numerator straight d squared straight S over denominator dr squared end fraction space equals fraction numerator 4 straight V over denominator straight h cubed end fraction plus 2 straight pi greater than 0 therefore space space space space space space straight S space is space minimum space when space straight h space equals space straight r space straight i. straight e. space height space space equals space radius space of space base.

Some More Questions From Application of Derivatives Chapter

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation