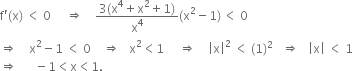Question
Find the intervals in which the function f is given by ![]()
(i) increasing (ii) decreasing
Solution
Here ![]()
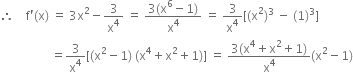
(i) For ![]() to be increasing
to be increasing
![]()
![]()
![]()
![]()
(ii) For f(x) to be decreasing,