Question
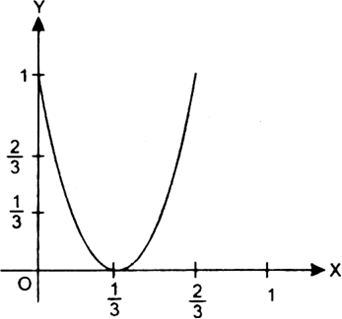
Find the maximum and the minimum values, if there be any, of f given by f(x) = 9x2 – 6x + 1, x ∊ R.
Solution
The given function is
f (x) = 9x2 – 6x + 1, x ∊ R
= (3x – 1) 2 ≥ 0, ∀ x ∊ R.
Also, f(x) = 0, if ![]() Therefore, the minimum value of f is 0 and the point of minimum value of f is Futher,f has no maximum value and hence no point of maximum value of in R.
Therefore, the minimum value of f is 0 and the point of minimum value of f is Futher,f has no maximum value and hence no point of maximum value of in R.