Application of Derivatives

Show that the curves 2x = y 2 and 2xy = k cut at right angles if k 2 = 8 - Wired Faculty

Question

Show that the curves 2x = y² and 2xy = k cut at right angles if k² = 8

Solution

The equation of two curves are
2x = y²...(1)
and    $2 xy space equals space straight k$ ...(2)
From (1) and (2), $straight y squared. space space straight y space equals space straight k space space space rightwards double arrow space space space space space straight y cubed space equals space straight k space space space space rightwards double arrow space space space straight y space equals space straight k to the power of 1 third end exponent$
$therefore space space space space from space left parenthesis 1 right parenthesis comma space space space space 2 straight x space equals space straight k to the power of 2 over 3 end exponent space space space space rightwards double arrow space space space space straight x space equals space 1 half straight k to the power of 2 over 3 end exponent$
$therefore$ point of intersection of curves (1) and (2) is $open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space straight k to the power of 1 third end exponent close parentheses$
From (1),    $2 space equals space 2 straight y dy over dx space space space space space rightwards double arrow space space space space space dy over dx space equals 1 over straight y$
$At space open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space space straight k to the power of 1 third end exponent close parentheses. space dy over dx space equals space 1 over straight k to the power of begin display style 1 third end style end exponent$
$therefore space space space space space space straight m subscript 1 space equals space 1 over straight k to the power of begin display style 1 third end style end exponent space where space straight m subscript 1 space is space slope space of space tangent space to space the space curve space left parenthesis 1 right parenthesis space at space the space point space of space intersection. space$
From (2),    $2 straight y plus 2 straight x dy over dx space equals space 0 space space space space space space rightwards double arrow space space space space dy over dx space equals space minus straight y over straight x$
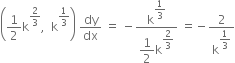
At $open parentheses 1 half straight k to the power of 2 over 3 end exponent comma space space straight k to the power of 1 third end exponent close parentheses space dy over dx space equals space minus fraction numerator straight k to the power of begin display style 1 third end style end exponent over denominator begin display style 1 half end style straight k to the power of begin display style 2 over 3 end style end exponent end fraction space equals negative 2 over straight k to the power of begin display style 1 third end style end exponent$
$therefore space space space space space straight m subscript 2 space equals space minus 2 over straight k to the power of begin display style 1 third end style end exponent space where space straight m subscript 2 space is space slope space of space tangent space to space the space curve space left parenthesis 2 right parenthesis space at space the space point space of space intersection.$
Curves (1) and (2) cut at right angles if $straight m subscript 1 straight m subscript 2 space equals space minus 1$
i.e., if $1 over straight k to the power of begin display style 1 third end style end exponent. space fraction numerator negative 2 over denominator straight k to the power of begin display style 1 third end style end exponent end fraction space equals negative 1$
i.e. if $straight k to the power of negative 2 over 3 end exponent space equals space 2 space space space space space space space space space straight i. straight e. space space space space if space space space space straight k squared space equals 8$
Hence the result.

For Daily Free Study Material Join wiredfaculty