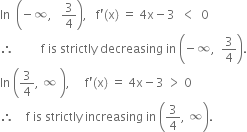Question
Find the intervals in which the function f given by f(x) = 2x2 – 3x is
(a) strictly increasing (b) strictly decreasing
Solution
f(x) = 2x2 – 3x ![]()
Now ![]()
The point ![]() divides the real line into two disjoint intervals
divides the real line into two disjoint intervals ![]() .
.