Question
Let I be any interval disjoint from (– 1, 1). Prove that the function f given by 
is strictly increasing on I.
Solution
Here 
Now, 
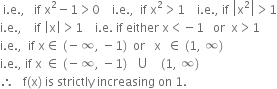
Let I be any interval disjoint from (– 1, 1). Prove that the function f given by is strictly increasing on I.
Here
Now,
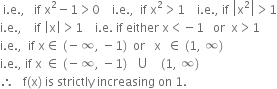
The radius of a circle is increasing uniformly at the rate of 4 cm per second Find the rate at which the area of the circle is increasing when the radius is 8 cm.
Mock Test Series
