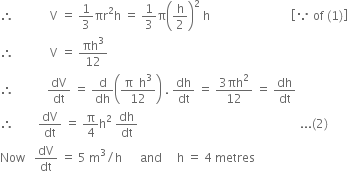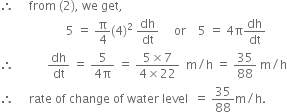+91-8076753736[email protected]
logo
logo
-->

Application Of Derivatives

Question
CBSEENMA12035033
Wired Faculty App

A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost. Its semi-vertical angle is tan–1 (0.5). Water is poured into it at a constant rate of 5 cubic metre per hour. Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4 m.

Solution

Let r be the radius, h be the height and a be semi-vertical angle of right circular cone. 
therefore space space space space tan space straight alpha space equals space straight r over straight h space space space or space space space straight alpha space equals space tan to the power of negative 1 end exponent open parentheses straight r over straight h close parentheses
But straight alpha space equals space tan to the power of negative 1 end exponent left parenthesis 0.5 right parenthesis                    (given)
therefore space space space space space straight r over straight h space equals space 0.5 space space space space space rightwards double arrow space space space space space straight r space equals space straight h over 2 space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis

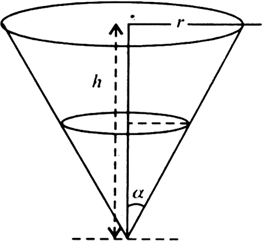
Let V be the volume of the cone. 
 therefore space space space space space space space space space space space space straight V space equals space 1 third πr squared straight h space equals space 1 third straight pi open parentheses straight h over 2 close parentheses squared space straight h space space space space space space space space space space space space space space space space space space space space space space space space space space space open square brackets because space of space left parenthesis 1 right parenthesis close square brackets therefore space space space space space space space space space space space space straight V space equals space πh cubed over 12 therefore space space space space space space space space space space space dV over dt space equals space straight d over dh open parentheses fraction numerator straight pi space space straight h cubed over denominator 12 end fraction close parentheses space. space dh over dt space equals space fraction numerator 3 πh squared over denominator 12 end fraction space equals space dh over dt therefore space space space space space space space space dV over dt space equals space straight pi over 4 straight h squared space dh over dt space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 2 right parenthesis Now space space space dV over dt space equals space 5 space straight m cubed divided by straight h space space space space space space and space space space space space straight h space equals space 4 space metres
therefore space space space space space from space left parenthesis 2 right parenthesis comma space we space get comma space space space space space space space space space space space space space space space space space space space space space space 5 space equals space straight pi over 4 left parenthesis 4 right parenthesis squared space dh over dt space space space space space or space space space space 5 space equals space 4 straight pi dh over dt therefore space space space space space space space space space space space dh over dt space equals space fraction numerator 5 over denominator 4 straight pi end fraction space equals space fraction numerator 5 cross times 7 over denominator 4 cross times 22 end fraction space space straight m divided by straight h space equals space 35 over 88 space straight m divided by straight h therefore space space space space space rate space of space change space of space water space level space space equals space 35 over 88 straight m divided by straight h.

Some More Questions From Application of Derivatives Chapter

The radius of a circle is increasing uniformly at the rate of 4 cm per second Find the rate at which the area of the circle is increasing when the radius is 8 cm.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation