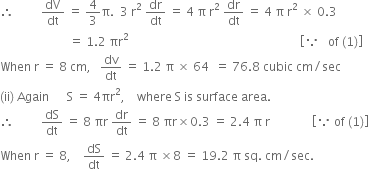Application of Derivatives

Question

The radius of a spherical soap bubble is increasing at the rate of 0.3 cms^–1. Find the rate of change of its (i) volume (ii) surface area when the radius is 8 cm.

Solution

Let r be the radius of spherical soap bubble
$therefore space space space space space space dr over dt space equals space 0.3 space space cms to the power of negative 1 end exponent space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$
(i) Now, $straight V equals 4 over 3 πr cubed space space space space space where space straight V space is space volume$
$therefore space space space space space space space space space dV over dt space equals space 4 over 3 straight pi. space space 3 space straight r squared space dr over dt space equals space 4 space straight pi space straight r squared space dr over dt space equals space 4 space straight pi space straight r squared space cross times space 0.3 space space space space space space space space space space space space space space space space space space space space space space space equals space 1.2 space πr squared space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space open square brackets because space space space of space left parenthesis 1 right parenthesis close square brackets When space straight r space equals space 8 space cm comma space space space dv over dt space equals space 1.2 space straight pi space cross times space 64 space space equals space 76.8 space cubic space cm divided by sec left parenthesis ii right parenthesis space Again space space space space space space straight S space equals space 4 πr squared comma space space space space where space straight S space is space surface space area. therefore space space space space space space space space space dS over dt space equals space 8 space πr space dr over dt space equals space 8 space πr cross times 0.3 space equals space 2.4 space straight pi space straight r space space space space space space space space space space space space space space open square brackets because space of space left parenthesis 1 right parenthesis close square brackets When space straight r space equals space 8 comma space space space space dS over dt space equals space 2.4 space straight pi space cross times 8 space equals space 19.2 space straight pi space sq. space cm divided by sec.$

For Daily Free Study Material Join wiredfaculty