+91-8076753736[email protected]
logo
logo
-->

Application Of Derivatives

Question
CBSEENMA12035065
Wired Faculty App

Find the slope of the tangent to the curve y = x3 – x + 1 at the point whose x-coordmate is 2.

Solution

The equation of curve is
                       straight y space equals space straight x cubed minus straight x plus 1
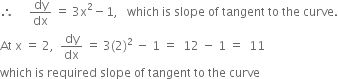
therefore space space space space space dy over dx space equals space 3 straight x squared minus 1 comma space space space which space is space slope space of space tangent space to space the space curve. At space straight x space equals space 2 comma space space dy over dx space equals space 3 left parenthesis 2 right parenthesis squared space minus space 1 space equals space space 12 space minus space 1 space equals space space 11 which space is space required space slope space of space tangent space to space the space curve

Some More Questions From Application of Derivatives Chapter

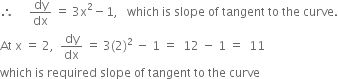
The radius of a circle is increasing uniformly at the rate of 4 cm per second Find the rate at which the area of the circle is increasing when the radius is 8 cm.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation