Application Of Derivatives

Question

A balloon which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the latter is 10 cm.

Solution

Let V be volume of balloon of radius r
$therefore space space space space space space straight V space equals space 4 over 3 πr cubed$
Rate of increase of volume w.r.t radius
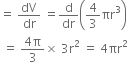
$WiredFaculty$
when r = 10 cm, rate of increase of volume = $4 space straight pi space left parenthesis 10 right parenthesis squared space equals space 400 space straight pi space cm cubed divided by cm$